De aquella charla —un tanto delirante, por cierto— dejé constancia en un relato que publicó Nevasport en este enlace. Lo que yo no podía sospechar es que después de aquel encuentro, la salud mental de Trustmi iba a emprender un camino de irreversible deterioro, como pude comprender nada más cruzar con él las dos o tres primeras frases.
—¡Hombre, Trustmi, tú por aquí! —le solté a modo de saludo.
Podría haber sido más original, lo sé, pero fue lo primero que se me ocurrió para disimular mi sorpresa por encontrármelo, después de tanto tiempo, en la biblioteca de la Escuela de Ingenieros de Caminos, escuela en la que yo era profesor y en la que Trustmi, que yo supiese, no había pasado nunca de primer curso. Precisamente en primero habíamos coincidido ambos de alumnos y habíamos trabado amistad; luego, los años nos habían hecho emprender trayectorias diferentes. Trustmi tenía demasiados intereses que no quería subordinar al objetivo de terminar la carrera. Yo, al principio, traté de animarlo a seguir; pero pronto comprendí que mis esfuerzos iban a ser baldíos porque lo que en realidad le apasionaba era esquiar, y la práctica intensiva del esquí, a la que se había entregado durante años, no parecía compatible con la dureza de los estudios de ingeniería. Poco a poco fuimos perdiendo el contacto. En los últimos tiempos, sólo sabía de él cuando me llegaba algún whatsapp suyo que, invariablemente, era una foto de esquí, normalmente de Vivi o de Cantbilifyu dejando firmas en palas de nieve virgen. Solo me enviaba las fotos, sin ningún comentario que las acompañase. A mi me gustaba verlas y, de hecho, las guardo todas en una carpeta aparte. He extraído dos al azar de esa carpeta, y las pongo a continuación.


Trustmi me miró y en su mirada había algo extraño. Pensé que no me había reconocido o que la vergüenza de seguir en primero cuando yo ya había terminado la carrera le hacía simular que no se acordaba de mí. Pero nada de eso: la expresión de sus ojos no era de despiste sino que estaba un punto por encima de la excentricidad y dos por debajo de la locura.
—¿Tú sabes lo que es una clotoide? — me soltó a bocajarro, sin molestarse en devolverme el saludo, como si nos hubiésemos visto por última vez hacía media hora.
Trastornado, pensé. Me lo temía, seguí pensando. Decidí seguirle el juego, así que respondí que sí, que es una curva de radio variable en la que el radio de curvatura disminuye en proporción inversa al camino recorrido sobre la curva.
—¡Exacto! De ecuación r*s=cte, siendo r el radio de curvatura y s el desarrollo a lo largo de la curva. ¡Qué bonita ecuación, y qué sencilla así expresada! Aunque no te creas, plantearla con ecuaciones que permitan representarla en coordenadas cartesianas tiene bastante tela. Bernoulli no consiguió una ecuación correcta y a Euler le llevó muchos años de trabajo caracterizarla completamente. ¡Y Euler era un genio!
¡Toma, y Bernoulli! Pensé sin decirlo. Miré por encima del hombro de Trustmi y vi que el libro que estaba consultando en la biblioteca tenía por título Trazado de carreteras. Así que por eso me había soltado lo de la clotoide, que se usa como curva de transición en el diseño de carreteras o vías de tren, con el fin de evitar discontinuidades en la aceleración centrípeta de los vehículos. La curva de transición que resulta tiene radio infinito en el punto tangente a la parte recta del trazado y el mismo radio de la circunferencia con la que se acuerda en el punto de tangencia; de esta manera el tipo de curva en carreteras es tramo recto-clotoide-circular-clotoide-tramo recto.
El nombre viene del griego κλοθειν / klothein : «hilar la lana». La misma raíz está en el nombre de Clotho, una de las tres Parcas, que teje el hilo de los destinos humanos, lo que evoca metafóricamente el hilo de lana que se enrolla indefinidamente alrededor del huso.
—Mira —prosiguió Trustmi, y me enseñó unas ecuaciones que había garabateado en una servilleta de papel que seguramente acababa de coger del bar de la Escuela. Saqué el móvil y le hice una foto a la servilleta, que reproduzco a continuación.
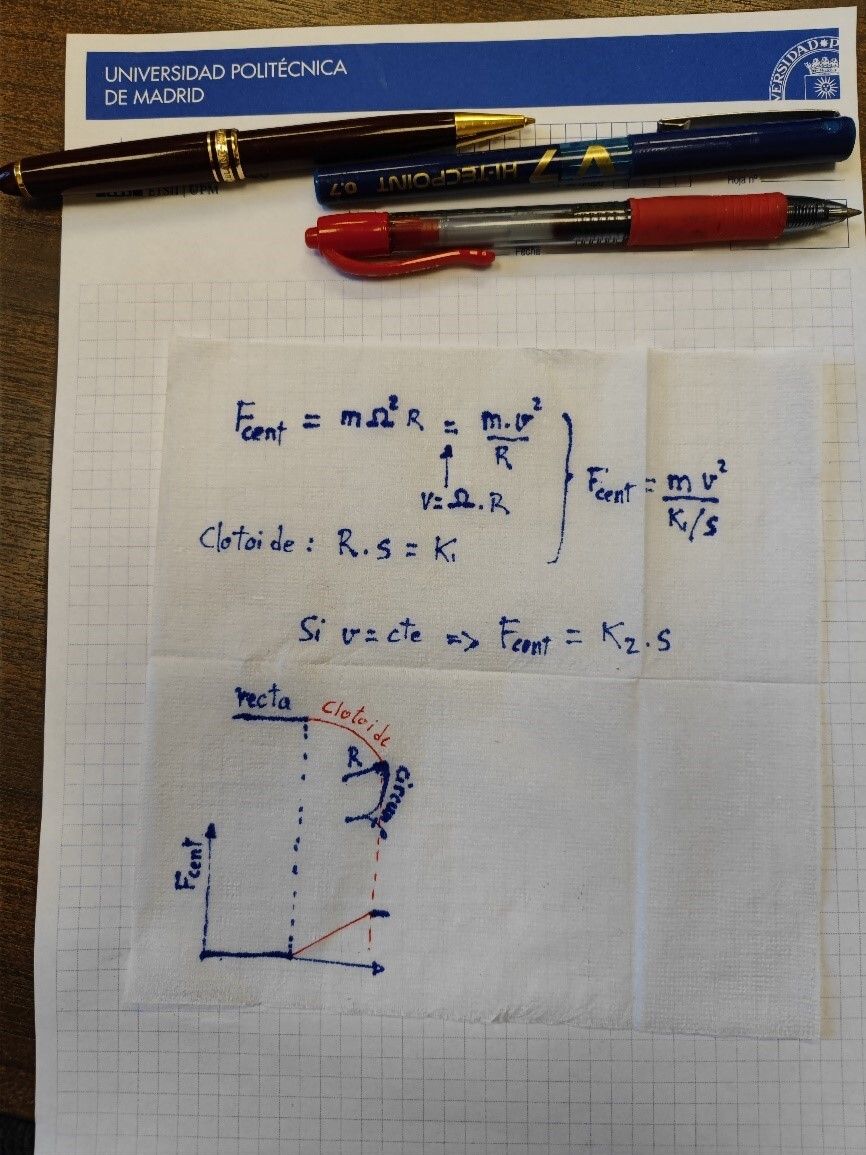
—Pero Trustmi —dije—, ¿No me dirás que ahora te ha dado por estudiar el trazado de las curvas en carretera?
Clavó en mí la mirada, y vi en sus ojos el mismo brillo que antes, pero algo más intenso. Quizás son dos puntos por encima de la excentricidad y solo uno por debajo de la locura, pensé.
—¿Carreteras? ¿Tú estás tonto? ¿Cómo que carreteras? ¿Qué carreteras ni qué carreteras? Lo que yo quiero saber de una puñetera vez es cómo se traza bien una curva esquiando. La culpa de todo la tiene el jodío Yoda, al que tú conoces porque estuvimos juntos en aquel bar de Baqueira, ¿te acuerdas?
Iba a contestar que sí, que me acordaba, pero Trustmi no me dejó interrumpirle y prosiguió diciendo:
—Aquella vez Yoda volvió a dar la tabarra con lo de las tres P: paciencia, progresividad y práctica, le gusta repetir. ¡Qué cabronazo! Lo suelta así y se queda tan pancho. Como si fuese fácil no ya hacerlo, sino tan solo comprenderlo. Lo de la práctica de acuerdo, tiene un pase. Pero las otras dos pes me han intrigado muchos años, hasta que el otro día se me ocurrió por fin cómo interpretarlo. Yo tal vez le cambiaría el orden: primero progresividad y luego paciencia. Fíjate en las ecuaciones. Lo que se ve en ellas es que en la clotoide la fuerza centrífuga aumenta linealmente. Fcent=K2*s. ¡Ahí está la clave de la progresividad! Sobre una clotoide en la que te desplazas a velocidad constante, la fuerza centrífuga empieza siendo nula al inicio del giro y luego va creciendo al recorrer la curva, hasta alcanzar un máximo justo antes de empezar a girar hacia el otro lado. Mira, te lo voy a dibujar.
Trustmi sacó un bolígrafo de color rojo y otro azul y dibujó en un papel (se ve que no tenía más servilletas) las dos siguientes curvas, que intentó que tuviesen forma de clotoide:

—El eje y es paralelo a la pendiente y el eje x perpendicular. ¿Qué crees que le pasa a la fuerza centrífuga que actúa sobre un esquiador que gira según una clotoide? ¡Exacto! Al inicio del giro, justo después del cambio de cantos, la fuerza centrífuga es muy pequeña, ya que el radio de curvatura es muy grande. Si en ese momento el esquiador sigue una trayectoria perpendicular a la línea de máxima pendiente (inicio de la curva roja), le toca empezar a meter peso en el nuevo esquí exterior para proyectarse de nuevo hacia la pendiente. Si lo hace incrementando la fuerza del apoyo manera progresiva, con el fin de curvar más el esquí, el radio de su curva se irá cerrando en forma de espiral, como si adoptase la forma de un anzuelo. Y la fuerza centrífuga irá creciendo progresivamente. Supongo que esa es la progresividad a la que se refiere el bueno de Yoda. ¿Hasta cuándo? Como dice Joma73, que también estaba aquel día en Baqueira, el momento idóneo para terminar el giro y empezar el siguiente es cuando se alinean dos de los vectores que intervienen: la gravedad y la fuerza centrífuga. Ese será el punto de tangencia entre la curva roja y la azul, en la que se repite la historia. Ahí es, creo yo, donde interviene la segunda P: hay que tener paciencia para terminar el giro, lo que hará bajar la componente de la velocidad paralela a la pendiente. De eso modo conseguimos no embalarnos.
El que miró ahora a Trustmi con ojos de loco fui yo. ¡Menuda chapa me había soltado! ¡Y eso que yo era el profe! Así que, un poco por tocarle los huevos y otro poco porque de verdad tenía curiosidad, le pregunté:
—Oye Trustmi, y todo eso... ¿para qué sirve?
—Pues no lo sé —repuso—. Tengo la sospecha de que para poco, porque, como dijo un sabio (Carolo, 2003), cuando esquías hay cosas que haces y otras que, simplemente, pasan. Y yo creo que esto de la clotoide es de las que pasan, si es que pasa, que bien podría ser que lo de la clotoide sea una alucinación mía. Aunque yo creo que, en esta foto, la esquiadora dibuja una trayectoria que se parece mucho a una clotoide.
Sacó su móvil y me enseñó otra foto de Vivi, que ya me había mandado en su día, aunque me cuidé mucho de decírselo.

Nuestro diálogo terminó de manera casi tan brusca como había empezado. Trustmi se levantó de golpe, hizo un guiñapo con la servilleta con las ecuaciones y el papel con los dibujos y los lanzó por el aire apuntando a una papelera cercana. Falló el tiro, tal vez porque el guiñapo dibujó una parábola y no una clotoide, como el pretendía. Sin molestarse en recoger del suelo los papeles, Trustmi dio media vuelta y se marchó sin despedirse. Sospecho que se fue directamente a intentar poner en práctica, con paciencia, lo de la progresividad.


